Generalidades de la Geometria Analitica

La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, continúa con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.

Las dos cuestiones fundamentales de la geometría analítica son:

• Dado la curva en un sistema de coordenadas, obtener su ecuación.

• Dada la ecuación indeterminada, polinomio, o función determinar en un sistema de coordenadas la gráfica o curva algebraica de los puntos que verifican dicha ecuación.

Lo novedoso de la geometría analítica es que representa las figuras geométricas mediante fórmulas del tipo , donde es una función u otro tipo de expresión matemática: las rectas se expresan como ecuaciones polinómicas de grado 1 (por ejemplo, ), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia , la hipérbola 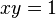), etc.