Conceptos Basicos de la Geometria Analitica

Una forma grafica para representar expresiones algebraicas es por medio del plano cartesiano, el cual consta de dos rectas numericas: una horizontal llamada eje de las abscisas o de las equis (x), y otra vertical llamada eje de las ordenadas o de las yes (y), las cuales se intersecan en un punto que recibe el nombre de origen, al que corresponde el punto O.

Esos dos ejes dividen al plano en cuatro regiones llamadas cuadrantes, que se numeran en sentido contrario al movimiento de las manecillas del reloj.



Como el plano cartesiano son dos rectas numericas, a la izquierda del origen, en el eje de las abscisas, se encuentran los valores negativos, y a la derecha los positivos. En el eje de las ordenadas, del origen hacia arriba, se encuentran los valores positivos y hacia abajo, los negativos, de donde resulta lo siguiente:

Primer cuadrante: abscisa positiva y ordenada positiva.

Segundo cuadrante: abscisa negativa y ordenada positiva.

Tercer cuadrante: abscisa negativa y ordenada negativa.

Cuarto cuadrante: abscisa positiva y ordenada negativa.

Puntos en el Plano Cartesiano

Un punto en el plano se localiza con una pareja ordenada de valores (x, y) llamados coordenadas, donde x es la primera componente y y la segunda. La primera componente (x) se localiza en el eje de las abscisas, y la segunda (y) en el eje de las ordenadas.

Al trazar las perpendiculares de cada uno de los ejes desde esos puntos, las lineas resultantes se intersecan en un punto que es el lugar buscado.

Si se tiene el par ordenado A (6, 2) y se localiza en el plano, la primera componente (6) se localiza en el eje de las abscisas y la segunda (2) en el eje de las ordenadas; al trazar la perpendicular de los ejes coordenados desde esos puntos se encuentra su interseccion, que es la coordenada A (6, 2).



En el par ordenado B (-7, 4) se puede observar que el valor de x es negativo y el de y es positivo, por lo que tal punto se localiza en el segundo cuadrante. Si el punto a localizar es C (--5, -2), el punto estara en el tercer cuadrante y si es D (8, -3), estara en el cuarto cuadrante.



Cuando la abscisa del par ordenado es 0, por ejemplo M (0, 5), el punto se localiza sobre el eje de las y. Y si la ordenada es 0, por ejemplo N (-7, 0) el punto se localiza en el eje de las x.



En ocasiones es necesario identificar las coordenadas de un punto observando su localizacion respecto al origen. Por ejemplo:



El punto A se localiza en la interseccion de las perpendiculares del eje de las abscisas en el punto 6 y del eje de las ordenadas en el 3; por lo tanto, sus coordenadas son (6, 3).

El punto B se localiza en la interseccion de las perpendiculares del eje de las abscisas en el punto -2 y del eje de las ordenadas en el -4, por lo tanto, sus coordenadas son (-2, -4).

En el plano cartesiano es posible representar expresiones algebraicas y su uso abarca no solo aspectos estrictamente matematicos sino tambien relativos a otras ramas de la ciencia.

Antecedentes Historicos de la Geometria Analitica

En el siglo XVII con la geometría analítica nace la matemática moderna, en el siglode Descartes, Galileo, Newton, Leibniz y Fermat. El álgebra y la trigonometría adquieren cierta madurez, condiciones particularmente favorables para la cienciamatemática obtenga una fecundidad maravillosa. Los resultados de tales condiciones favorables pronto se harán sentir, y en sigloXVII verá en primer lugar una admirable nueva rama de la matemática: lageometría analítica, que produce en esa ciencia verdadera revolución (fue comparada con la revolución industrial). En el siglo XVII asiste al nacimiento de la teoría de los números, del calculo de laprobabilidad y de la geometría proyectiva.

La geometría analítica es la rama de la geometría en la que las líneas rectas, las curvas y las figuras geométricas se representan mediante expresiones algebraicas y numéricas usando un conjunto de ejes y coordenadas. Cualquier punto del plano sepuede localizar con respecto a un par de ejes perpendiculares dando las distancias delpunto a cada uno de los ejes. La geometría analítica fue inventada por René Descartes (1596 - 1650), trabajaproblemas geométricos a base de un sistema de coordenadas y su transformación aproblemas algebraicos. Se subdivide en geometría analítica plana, para ecuaciones condos variables, y geometría analítica sólida, para ecuaciones con tres variables.

La geometría analítica se conoce también con el nombre de geometría cartesiana.

Generalidades de la Geometria Analitica

La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, continúa con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.

Las dos cuestiones fundamentales de la geometría analítica son:

• Dado la curva en un sistema de coordenadas, obtener su ecuación.

• Dada la ecuación indeterminada, polinomio, o función determinar en un sistema de coordenadas la gráfica o curva algebraica de los puntos que verifican dicha ecuación.

Lo novedoso de la geometría analítica es que representa las figuras geométricas mediante fórmulas del tipo , donde es una función u otro tipo de expresión matemática: las rectas se expresan como ecuaciones polinómicas de grado 1 (por ejemplo, ), las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (la circunferencia , la hipérbola 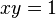), etc.